Свойство выпуклости каждой связной компоненты подмножества X из ℝn (или из любого векторного пространства) можно сформулировать на языке приведенных нульмерных групп гомологий. А именно, такое свойство равносильно тому, что для всякой прямой l ⊂ ℝnиндуцированный вложением гомоморфизм
![]()
является инъективным; последнее и означает, что если две точки из X можно соединить путем в X, то это же можно сделать на прямой l, проходящей через точки. Назвав множества с таким свойством 0-выпуклыми, естественным покажется следующее
Определение. Подмножество X ⊂ ℝn называется (k - 1)-выпуклым, если для всякой k-мерной плоскости π ⊂ ℝn индуцированный вложением гомоморфизм
![]()
является инъективным.
Для формулировки основного результата о выпуклости дополнения напомним, что алгебраическое подмножество V ⊂ Tn называют приведенным полным пересечением коразмерности k, если оно может быть задано в виде
где dP1 ∧ . . . ∧ dPk ⁄≡ 0 на каждой неприводимой компоненте V .
Имеет место следующая
Теорема. [8] Дополнение амебы алгебраической поверхности коразмерности k является (k - 1)-выпуклым.
Эту теорему поясняет рис. 3.1: 1-цикл γ, выбранный в сечении плоскостью π в дополнении к амёбе, не гомологичен нулю в этом сечении. Он остается не гомологичным нулю в дополнении амёбы из-за того, что щупальцы уходят на бесконечность с некоторыми асимптотами.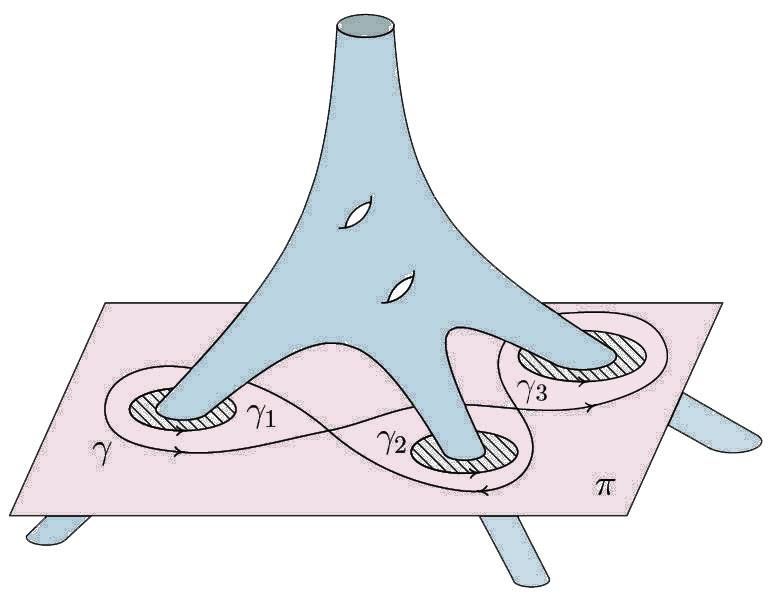
3.1.