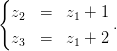Рассмотрим комплексную прямую в ℂn:
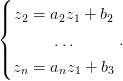
Контуром ее амебы по определению является множество критических значений логарифмического отображения
![]()
Для нахождения контура необходимо вычислить матрицу якоби отображения Log в координатах z1,z1:
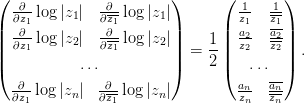
Условием критичности, т.е. немаксимальности ранга вычисленной матрицы, будет переопределенная система уравнений:
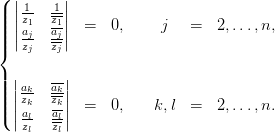
(3. 2)
Справедлива следующее утверждение: Контур амебы комплексной прямой в ℂn,n > 2, задаваемой уравнениями
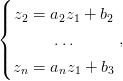
все aj,bj≠0, непуст тогда и только тогда, когда
![]()
(3. 3)
При этих условиях контур амебы представляет собой образ вещественной прямой d2x = c2y на комплексной плоскости переменного z1 = x + iy при отображении Log.
Любое из условий существования контура амебы в (3.3) можно считать выполненным, если хотя бы один из входящих в него коэффициентов равен нулю. Для bj = 0 это видно из системы (??), а для ak = 0 — из условий (3.2).
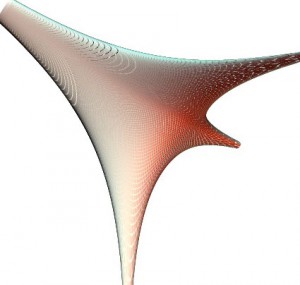
Пример. Рассмотрим прямую
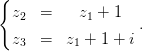
(3. 4)

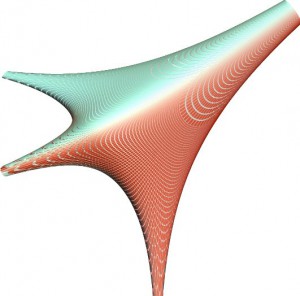


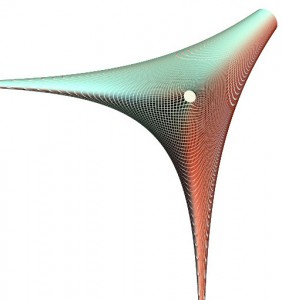

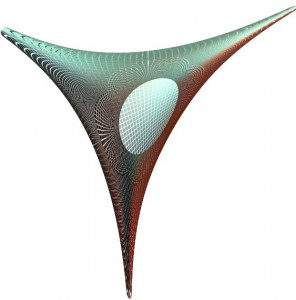
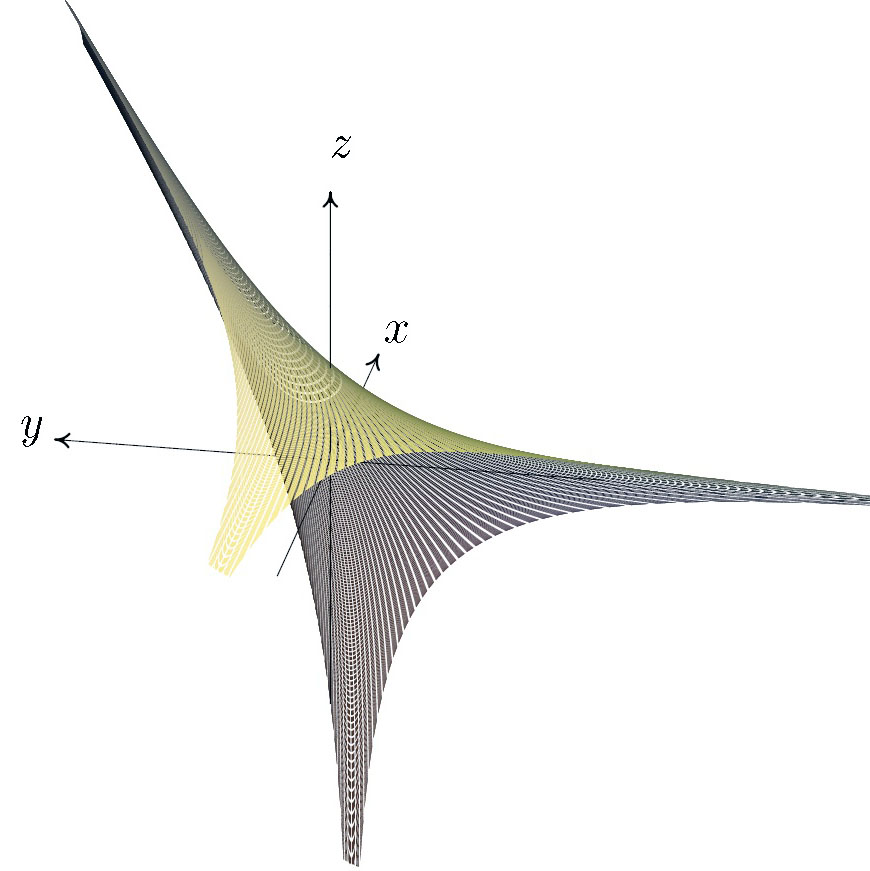
Пример. Случай, когда отношение ![]() вещественно, изображен на рис. 3.5. Это амеба прямой
вещественно, изображен на рис. 3.5. Это амеба прямой
(3. 5)
Отношение ![]() в этом случае равно 2. Амеба представляет собой поверхность с краем в ℝ3, каждая внутренняя точка которой имеет по два прообраза на исходной прямой (3.5):
в этом случае равно 2. Амеба представляет собой поверхность с краем в ℝ3, каждая внутренняя точка которой имеет по два прообраза на исходной прямой (3.5):
![]()
Таким образом, по сравнению с невырожденным случаем эта амеба «схлапывается» — противоположные точки поверхности слипаются в одну.
Контуром такой амебы является ее край, прообразом которого в данном случае будет вещественный срез плоскости переменного z1.
3.5
Пример 1. Наконец, если хотя бы один из коэффициентов в уравнениях прямой обращается в ноль, то амеба «ложится» в плоскость в ℝ3 и в этой плоскости представляет собой амебу комплексной прямой с заведомо непустым контуром. Такой вид, например, имеет амеба прямой
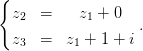
(3 .6)
Отметим, что приведенные примеры описывают все возможные классы амеб комплексной прямой и для n-мерной ситуации (кроме крайне вырожденного случая, когда все zj пропорциональны и амеба комплексной прямой представляет собой вещественную прямую в ℝn).