Обозначим через Tn комплексный алгебраический тор 
n. Рассмотрим в Tn полином Лорана
(2.1)
где A ⊂ ℤn — конечное множество.
Определение. Многогранником Ньютона Δf полинома f(z) называется выпуклая оболочка всех показателей α = (α1,…,αn) мономов zα входящих в f(z).
Множество нулей полинома f определяет алгебраическую гиперповерхность V = {f = 0}. Напомним, что амебой этой гиперповерхности (или полинома f) мы называем ее образ Af относительно логарифмического отображения Log : Tn → ℝ, действующего по формуле
Как уже отмечалось, Log является собственным отображением, поскольку прообразом каждой точки амебы является компактное множество — тор:
Поэтому амеба Af замкнута как образ замкнутого множества, а её дополнение открыто. Дополнение ℝn \Af состоит из связных компонент E, каждая из которых открытая и выпуклая. Пусть E — связная компонента дополнения ℝn \Af.
Нам потребуются два фундаментальных понятия из выпуклого анализа.
Определение. Конус рецессии выпуклого множества E — это наибольший конус, который можно поместить в E некоторым сдвигом.
Определение. Двойственным конусом к многограннику Δf в точке v ∈ Δf называется множество
Связь между комбинаторикой многогранника Ньютона Δf полинома Лорана f и структурой дополнения ℝn \Af дает следующая
Теорема. [66] Пусть V = 
— гиперповерхность в Tn. Тогда на множестве компонент связности дополнения ℝn \Af существует инъективная функция порядка
такая, что двойственный конус Cν(E)∨ к многограннику Ньютона есть конус рецессии компоненты E. Целочисленный вектор ν(E) называется порядком компоненты E.
Согласно этой теореме, существует взаимно-однозначное соответствие между множеством связных компонент {E} дополнения к Af и некоторым подмножеством целочисленных векторов ν ∈ Δf. Тем самым, дополнение ℝn \Af состоит из конечного числа связных компонент, и эти компоненты идентифицируются векторами ν ∈ ℤn ∩ Δ f. Таким образом, каждая связная компонента из ℝn \Af идентифицируется записью Eν, где ν ∈ ℤn ∩ Δ f.
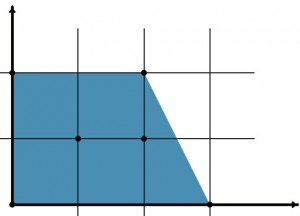
На рисунке 2.4 приведены многоугольник Ньютона многочлена f(z1,z2) = 1 + z12z 2 + z1z22 - 4z 1z2 и соответствующие компоненты дополнения его амебы. На рисунке 2.5 изображены многоугольник Ньютона для произведения трех аффинных функций общего положения и соответствующие компоненты дополнения амебы этого произведения.
ункция порядка ν(E) допускает несколько реализаций. По одной из них, ν(E) равна градиенту функции Иенсена-Ронкина Nf(x) на E (напомним, что эта функция аффинно-линейна на E):
Другая интерпретация состоит в том, что координата νj вектора ν = ν(E) равна коэффициенту зацепления гиперповерхности V = {f = 0} с базисной петлей ej вещественного тора {|zj| = exj,j = 1,…,n},x ∈ E. Существует также интегральное представление для νj.
В случае двух переменных Δf — многоугольник в ℝ2. Целые точки ν ∈ Δf ∩ ℤ2 могут быть трех видов: вершины Δ f; точки, лежащие в относительной внутренности сторон Δf и, наконец, внутренние точки Δf. Конусом рецессии компоненты Eν в этих случаях будут соответственно, плоский двумерный конус, луч и точка.
Из приведенной теоремы вытекает
Следствие. Число связных компонент дополнения ℝn\Af не меньше числа вершин Δf и не больше числа целых точек Δf:
Таким образом, многогранник Ньютона Δf в некоторой мере отражает структуру амебы Af гиперповерхности, определяемой нулями f в торе Tn. Однако информации о комбинаторике многогранника недостаточно для того, чтобы полностью охарактеризовать амебу Af. Дело в том, что при разных значениях коэффициентов cα в f(z) компоненты дополнения с вырожденными (неполномерными) конусами рецессии могут открываться, а могут и не высвечиваться. Согласно результату [57], для любого подмножества Δf′ из Δ f, содержащего множество вершин vertΔf, существует набор коэффициентов, для которого дополнение ℝn \Af имеет лишь связные компоненты Eν, соответствующие ν ∈ Δf′.
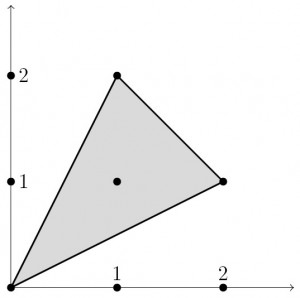
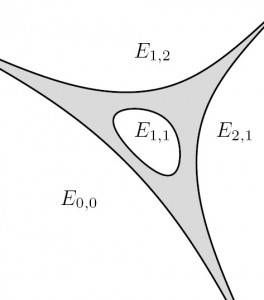
2.4.
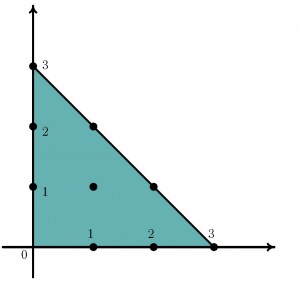
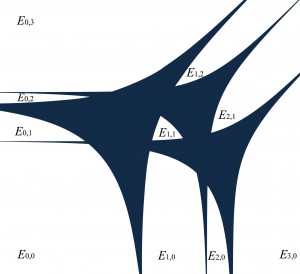
2.5.
На рисунках 2.4 и 2.5 изображены амёбы Af, в дополнении которых имеются все связные компоненты, соответствующие всем целым точкам многогранников Ньютона Δf.
Следует отметить, что в размерности n = 2 ограниченным компонентам,т.е. дыркам, соответствуют внутренние целые точки многоугольника Ньютона. Например, у амебы кривой, изображенной на рис. 2.6, задаваемой многочленом 1 + z13 + z 12z 22 + az 1z2 + bz12z 2 есть две «дырки», соответствующие двум внутренним точкам ее многоугольника Ньютона. Компонентам, которые содержат ненулевые углы, соответствуют вершины многоугольника. Остальным компонентам соответствуют целые точки из относительной внутренности границы многоугольника.
2.6. Амеба комплексной кривой в ℂ2 и многоугольник Ньютона определяющего её полинома