Для n = 2 существует более рациональный способ построения графика, основанный на подразбиении многоугольника Ньютона.
Определение. Δp тропического многочлена pt(x) вида 4.1 называется выпуклая оболочка всех показателей i = (i1,…,in) мономов xi входящий в p t(x).
При n = 2 Δpt называется многоугольником Ньютона.
Введем понятие подразбиения многоугольника Ньютона Δpt.
Поставим в соответствие каждому члену aij ⊙ xiyj из p t(x) точку (i,j,aij) в ℝ3. Построим выпуклую оболочку всех точек (i,j,a ij) и рассмотрим проекцию:
![]()
Результат проектирования и есть многоугольник Ньютона Δpt вместе с его подразбиением.
Теорема. Тропическая кривая V pt двойственна подразбиению многоугольника Ньютона Δpt, а именно лучи кривой ортогональны сторонам многоугольника, а внутренние отрезки кривой - отрезкам подразбиения многоугольника Ньютона.
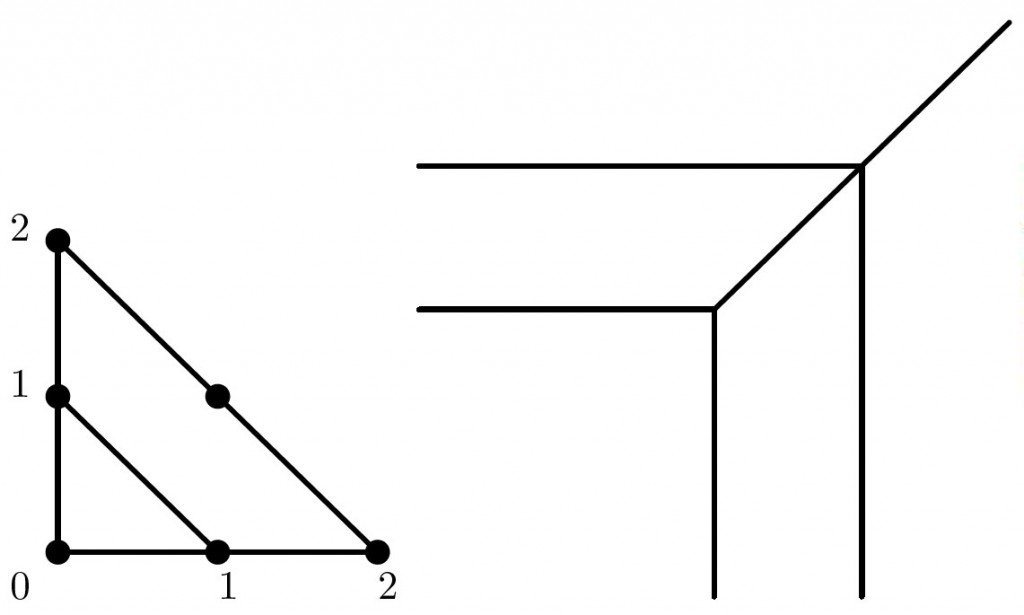
Пример. Рассмотрим полином первой степени pt(x,y) = A⊙x⊕B⊙ y⊕C. Его многоугольник Ньютона изображен на рисунке 4.3 и не имеет подразбиений.
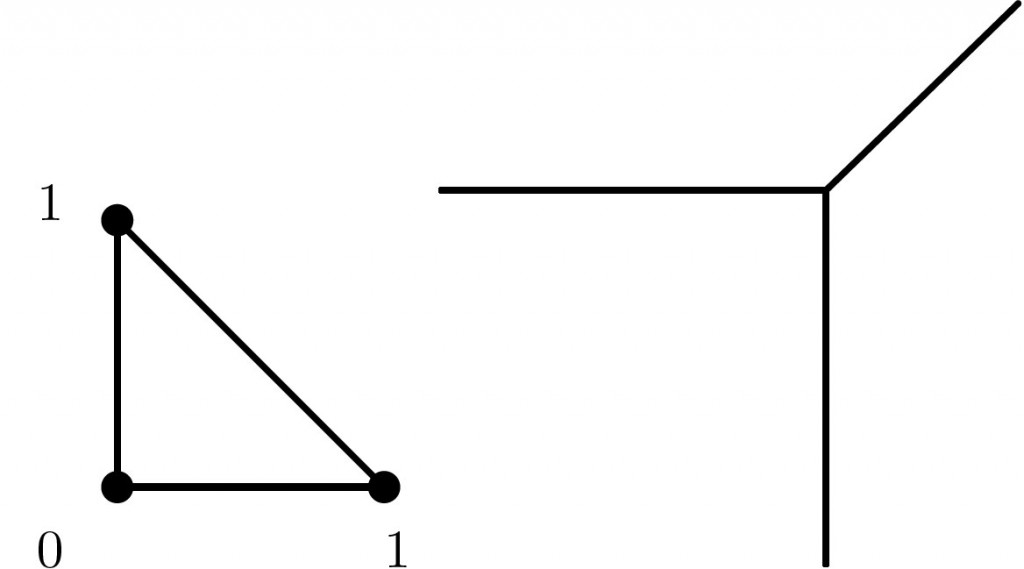
Рис. 4.3. Подразбиение Δpt, кривая V pt и график для pt(x,y) = A ⊙ x ⊕ B ⊙ y ⊕ C
Подразбиение Δpt возможно, когда он содержит целые точки, отличные от вершин.
Пример. Рассмотрим произвольный тропический полином второй степени
![]()
(4.4)
С точки зрения классической арифметики этот полином определяет кусочно-линейную функцию
![]()
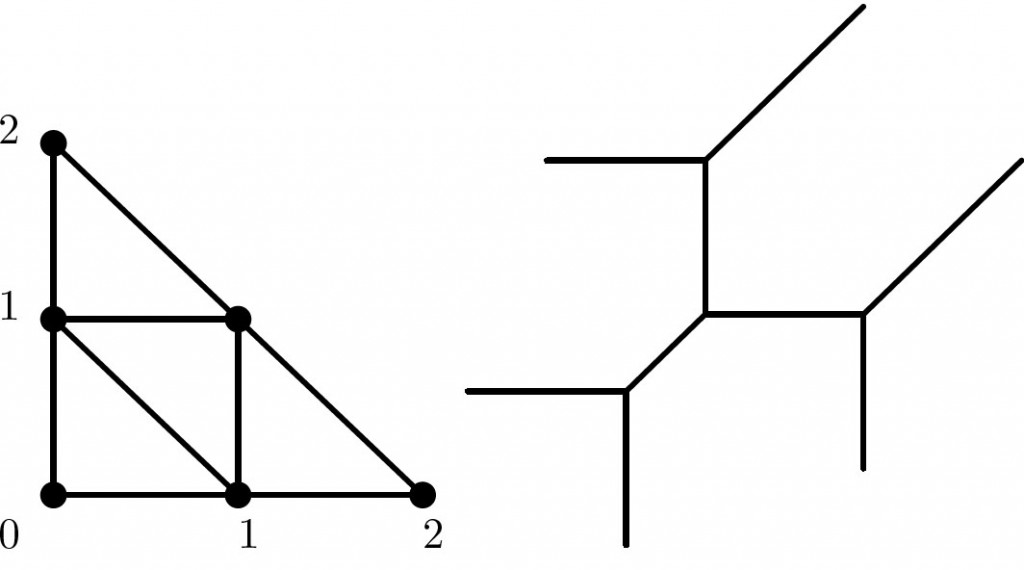
Многоугольником Ньютона многочлена 4.4 является треугольник, содержащий целые точки на сторонах. В зависимости от значения коэффициентов возможно одиннадцать подразбиений и, соответственно, одиннадцать типов форм тропических кривых. Некоторые из них изображены на рис. 4.4 и рис. 4.5.
Рис. 4.4. Подразбиение Δp, кривая V (pt) и график для p(x,y) = x⊙2 ⊕ x ⊙ y ⊕ y⊙2 ⊕ 2 ⊙ x ⊕ 2 ⊙ y ⊕ 2
Рис. 4.5. Подразбиение Δp, кривая V (pt) и график для p(x,y) = 0 ⊙ x⊙2 ⊕ 2 ⊙ x ⊙ y ⊕ 0 ⊙ y⊙2 ⊕ 2 ⊙ x ⊕ 2 ⊙ y ⊕ 0
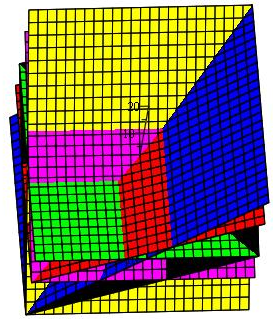
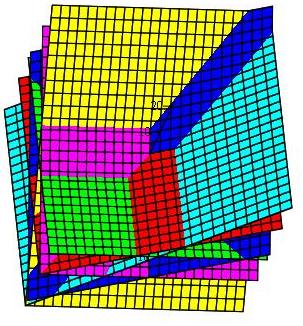
Заметим, что тропическую кривую легко построить, используя систему компьютерной математики Maple. Для построения графиков в Maple необходимо подключить пакеты plots и plottools. Для построения графиков в тропической кривой используем функцию из пакетаplots — plot3d, для которой необходимо задать функцию, график которой требуется построить, область определения x и y.
Для построения поверхностей используется команда
где expr — функция, график которой необходимо построить; x = a..b — область определения переменной x; y = c..d — область определения переменной y. В качестве опций можно изменять такие параметры, как вид координатных осей axes, цвет графика color, сетка на плоскости grid и др. Для отображения нескольких графиков в одной плоскости используется команда display.
Рис. 4.6. Построение тропической кривой p(x,y) = x⊙2 ⊕y⊙2x⊙y⊕2⊙x⊕y⊕0 в математическом пакете Maple 13