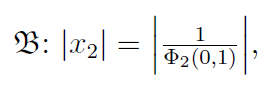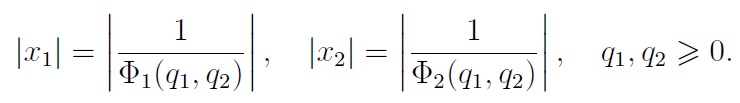Степенные ряды (ряды Тейлора, Лорана, Пюизо) сходятся вплоть до «ближайших» особенностей аналитических функций, которые они представляют. Согласно Лемме Абеля, области сходимости степенных рядов являются n-круговыми, тем самым, они определяются лишь условиями на модули переменных.
Определение 1. Степенной ряд
называется гипергеометрическим (по Горну), если отношения
являются рациональными функциями переменных суммирования.
Гипергеометрический ряд в своей области сходимости представляет лишь некоторый аналитический элемент (ветвь) многозначной функции с сингулярностями на алгебраическом множестве. Поэтому некоторые фрагменты сингулярного множества могут пересекать область сходимости ряда, являясь сингулярностями других ветвей.
Здесь мы проиллюстрируем взаимное расположение сингулярного множества относительно области сходимости. При этом языком такого описания будут амебы сингулярного множества.
Заметим, что гипергеометрические ряды с непустой областью сходимости имеют много нулевых коэффициентов φ(s), а именно, для них реальное суммирование ведется не по всей решетке ℤn, а лишь по некоторому заостренному конусу.
Горн разработал метод описания областей сходимости гипергеометрических рядов двух и трЈех переменных, рассматривая в качестве конуса (носителя) суммирования положительные октанты ℤ+2 и ℤ +3. Приведем результат Горна для двойных рядов
где, по определению гипергеометричности, отношения
являются рациональными функциями от s1 и s2.
Горном вводятся пределы
и отмечается, что функции Φi рациональны и однородны степени нуль, то есть, фактически зависят от отношения q1 : q2. C помощью этих функций и вычисляется область сходимости G ряда H(x1,x2). А именно, как отмечалось выше, области сходимости степенных рядов являются областями Рейнхардта, то есть, полностью определяются модулями |x1|,|x2| переменных. Согласно результату Горна, если точка (|x1|,|x2|) лежит на границе изображения Рейнхардта |G| для области сходимости G, то она лежит или на прямой
или на прямой
или на кривой G, в параметризованном виде
(5.1)
Следующие примеры дают наглядную интерпретацию взаимного расположения областей сходимости гипергеометрических рядов и сингулярных множеств функций, представляемых этими рядами.
Пример 1.
Этот пример взят из статьи Горна [15]:
![]()
(5.2)
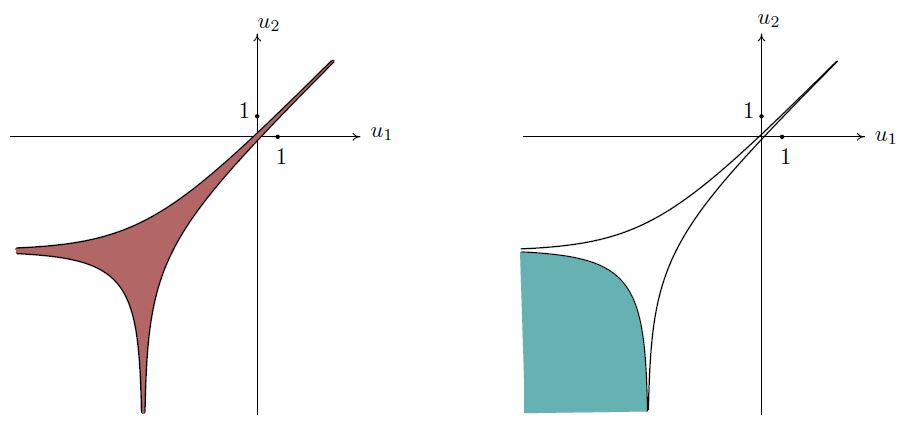
где a1,a2,a3 – произвольные комплексные числа, для которых значения гамма функций конечны. Согласно результату Горна, изображение области сходимости указанного ряда на схеме Рейнхардта ограничено тремя линиями (см. рис. 3 слева):
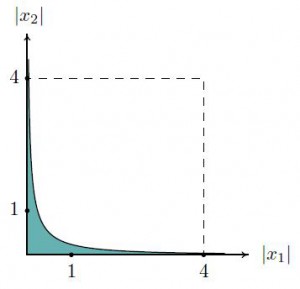
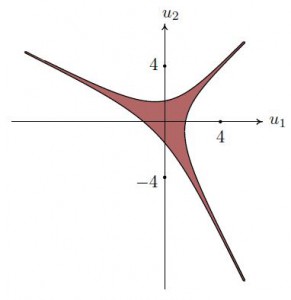
3 Изображение области сходимости ряда (5.2) на диаграмме Рейнхардта (слева). Амеба особенности суммы ряда (5.3) (справа)
Уравнения этих линий:
![]()
![]()
Заметим, что все множество под гиперболической кривой G – это область сходимости «подряда» ряда (5.2) с носителем суммирования
![]()
а не ряда с полным носителем ℤ+2, который Горн взял»насильно».
На рис. 3 в системе координат u1 = log |x1|,u2 = log |x2| изображена амеба для сингулярного множества суммы «подряда»
![]()
(5.3)
ряда (5.2). Само сингулярное множество параметризуется подобно формуле (5.1), но без модулей, причем q1 : q2 пробегает всю комплексную прямую
![]()
(5.4)
Область сходимости «подряда» проектируется в связную компоненту дополнения к амебе, затемненную на рис. 5 (слева). Эта компонента получается пересечением всех полуплоскостей, лежащими под касательными к Log-образу куска кривой G, для которого параметр qпробегает сектор S. Каждая полуплоскость представляет собой Log-образ области сходимости диагонального подряда с суммированием по лучу {s = lq : l ∈ ℝ+}. А область сходимости ряда (5.2) проектируется лишь в часть этой компоненты (см. рис. 5 (справа)), выделенную условием u1 < log 4,u2 < log 4. Эта часть получается пересечением всех полуплоскостей, лежащими под касательными к куску G, определенному условием q ∈ ℝ+2.
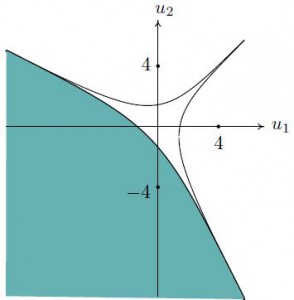
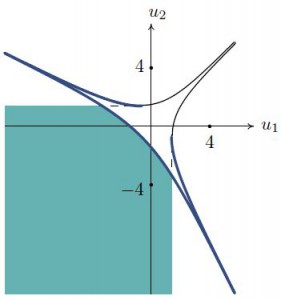
5 Log-образы областей сходимости рядов (5.3) и (5.2)
Пример 2. В работе [5] вычислен фундаментальный период трехмерного многообразия Калаби-Яу в виде гипергеометрического ряда Горна:
![]()
(5.5)
Для этого ряда вектор Горна следующий:
![]()
Заметим, что граница области сходимости ряда (5.5) задается уравнением
![]()
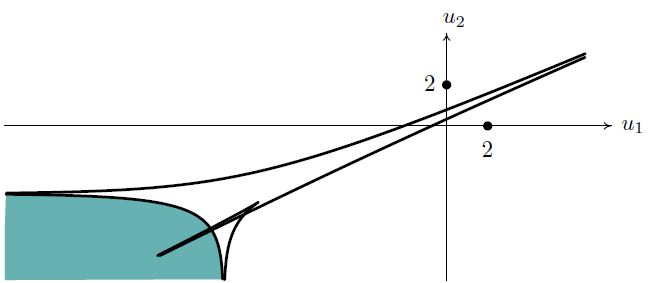
Область сходимости ряда (5.5) представлена рисунком 6, а на рис. 8 изображена амеба для сингулярного множества этого ряда.
6 Область сходимости ряда H2(x1,x2) При этом затемненная компонента дополнения этой амебы и есть область сходимости ряда (5.5) в логарифмических координатах.
8 Амеба сингулярного множества для ряда H2(x1,x2) (слева) и область сходимости ряда (справа)
Пример 3. В работе [7] рассмотрен многочлен
![]()
определяющий во взвешенном проективном пространстве ℙ(3,2,2,7,7)4 гиперповерхность Калаби-Яу. В подходящих координатах (которые мономиально выражаются через модули деформации поверхности P(y) = 0) фундаментальный период гиперповерхности представляется рядом
![]()
Граница области сходимости этого ряда допускает параметризацию
![]()
Сама область сходимости в логарифмической шкале на рис. 10 закрашена. Она примыкает к амебе сингулярного множества, затемненной на рис. 9. Здесь мы наблюдаем ситуацию, когда сингулярное множество полной аналитической функции, порожденной рядом, пересекает область сходимости ряда
9 Амеба сингулярного множества для H3(x1,x2)
Рисунок 10 Область сходимости ряда H3(x1,x2) в логарифмической шкале