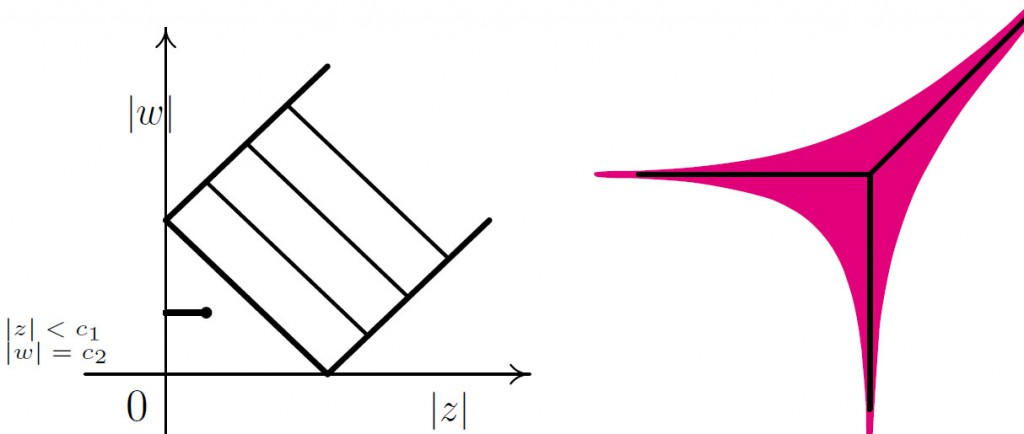
Пример. Классическим и самым простым примером является амеба комплексной прямой, определяемая нулями полинома f(z) = az+bw+c. Многоугольник Ньютона Δf в этом случае не содержит иных целых точек, кроме вершин ( это треугольник с вершинами (0, 0), (0, 1), (1,0)), поэтому, согласно Следствию 1, у Af будет всего 3 компоненты дополнения E00,E10,E01 . Из соображения тропической геометрии спайн амебы — трехрожник (см. рис. 4.7).
4.7. Кривая V = z + w - 1 = 0 на схеме Рейнхардта, ее амеба V и ее спайн
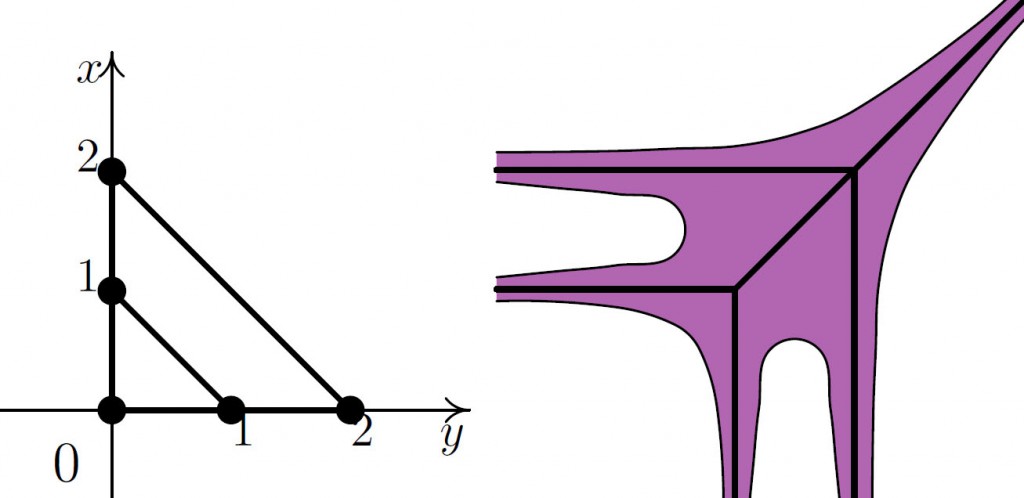
ример. Пусть f(z) = 1 + z + w + ![]() +
+ ![]() . Кривая V = {f(z) = 0}, ее амеба и спайн рассматривались в статье [49]. В этой статье показано, что полином Sf для этого случая будет иметь вид:
. Кривая V = {f(z) = 0}, ее амеба и спайн рассматривались в статье [49]. В этой статье показано, что полином Sf для этого случая будет иметь вид:
![]()
где a(1,0) = a(0,1) = ln(3 -![]() ). Амеба кривой V и ее спайн изображены на рисунке 4.8.
). Амеба кривой V и ее спайн изображены на рисунке 4.8.
4.8. Δf, амеба и спайн кривой, определяемой полиномом 1 + z + w + ![]() +
+ ![]()
Пример. Исследование амеб тесно связно с локальными геометриями Колаби-Яо, которые моделируют калибровочные теории в физике. Важным примером в рамках U(1) теории является амеба полинома Лорана, имеющего вид
![]()
(4.8)
Полином f имеет многоугольник Ньютона, изображенный на рисунке 4.9.
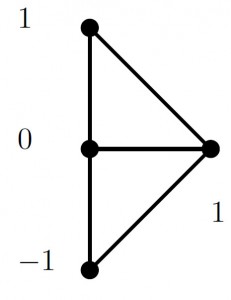
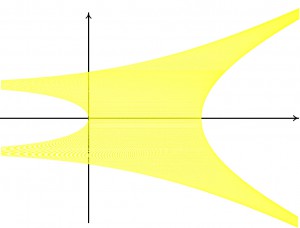
4.9. Многоугольник Ньютона Δf полинома f(z,w) = z - 5 - 2(w + w-1), амеба определяемой им кривой и ее спайн.
Полином SAf имеет вид
![]()
где, коэффициент c00 = ln 4.
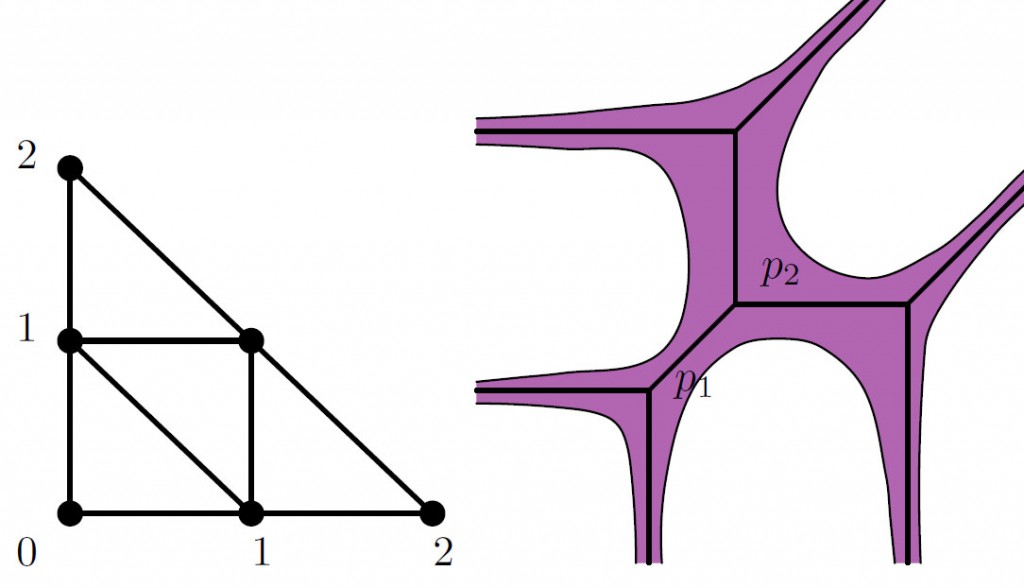
Пример. В некоторых задачах возникает необходимость рассматривать амебы, которые имеют максимальное число связных компонент в дополнении (см., например, [29]). Мы ограничимся рассмотрением случая n = 2 и кривой
![]()
(4.9)
Если у амебы Af, определяемой полиномом 4.9 открыты все компоненты дополнения Eα, то она имеет вид, изображенный на рисунке 4.10.
4.10. Δf, амеба и спайн SAf кривой, определяемой полиномом f(z1,z2) = Az12 + Bz 22 + Cz 1z2 + Dz1 + Ez2 + F.
Пусть f(z1,z2) имеет вид 4.9 где A,B,C,D,E,F — комплексные числа, причем A,B,F не равны нулю. Тогда тропический полином Sf, определяющий спайн амебы, имеет вид:
![]()
где
![]()
![]()
![]()