Как мы видели, амеба алгебраической гиперповерхности наследует много информации от многогранника Ньютона, определяющего гиперповерхность многочлена. Что же произойдет, если мы заменим многочлен на ряд?
Итак, пусть Q – ненулевой ряд Лорана, зависящий от переменных
z = (z1,…,zn):
![]()
т.е. теперь сумма является бесконечной. Естественно, что в этом случае попытка определить амебу нулей этого ряда, должна сопровождаться несколькими допущениями.
Прежде всего, чтобы c рядом можно было работать неформально, предположим, что его область абсолютной сходимости G непустая.
Поскольку ряд может вообще не иметь нулей, мы также будем предполагать, что Q имеет нули в G ∩ Tn. Пусть
![]()
– гиперповерхность нулей функции Q(z). Тогда амеба для V определяется также, как и в алгебраическом случае: AV = Log(V ).
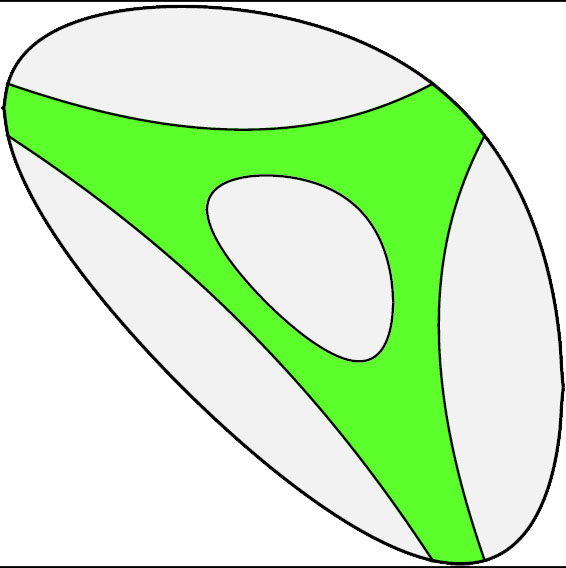
Теперь нам необходимо разобраться в какой среде обитает амеба комплексной гиперповерхности. В алгебраическом случае, когда Q – полином, естественным ареалом обитания амебы было все вещественное n-мерное пространство ℝn. В произвольном же случае ареал ограничен областью сходимости ряда (см. рисунки 2.9 и 2.10).
2.9. Амеба комплексной гиперповерхности выделена зеленым цветом, а логарифмический образ области сходимости G – серым.
Введем обозначение
для образа области сходимости G ряда Q. Это и будет множество, вмещающее амебу. Из комплексного анализа хорошо известно, что области сходимости степенных рядов являются логарифмически выпуклыми, поэтому G – выпуклая область. В алгебраическом случае G совпадает со всем ℝn, а амеба AV является собственным подмножеством в G c открытым дополнением. В общем случае это не так, и может иметь место равенство AV = G. Чтобы исключить эту ситуацию, потребуем, чтобы носитель A ряда Q лежал в некотором заостренном конусе, т.е. чтобы замыкание N выпуклой оболочки ch(A) не содержало прямых.
Множество N является аналогом многогранника Ньютона в неалгебраическом случае. Оно представляет собой полиэдральный конус, который уже может быть и нерациональным.
Следующее утверждение позволяет извлечь некоторую информацию о дополнении G\AV непосредственно из конуса N.
Теорема. [51] Если для ряда Q множество N =ch(A) не содержит прямых, то дополнение G \ AV ≠∅. Множеству вершин ν многогранника N соответствует семейство попарно различных связных компонент E = Eν дополнения G\AV .
На рисунке 2.9 изображена амёба для случая, когда множество вершин конуса N является пустым, поскольку конус совпадает со всем ℝ2. Амёба, изображенная на рисунке 2.10, соответствует случаю, когда N = ℕ≥02, т.е. содержит две вершины (0, 1) и (1, 0). Точнее на Рис. 2 изображена амеба ряда ∑ (α1,α2)∈ℕ2z1α1z 2α2.
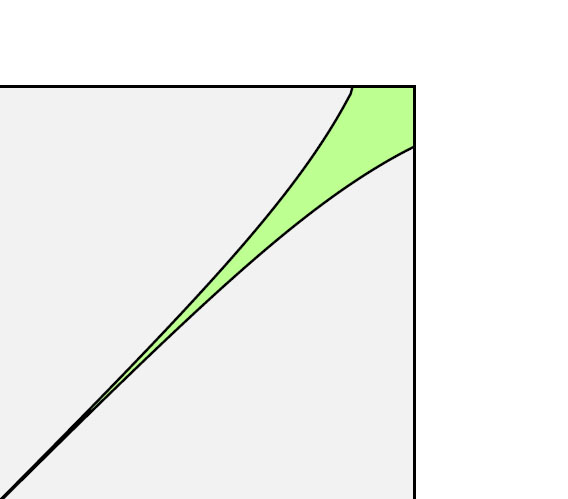
2.10. Амеба комплексной гиперповерхности выделена зеленым цветом, а логарифмический образ области сходимости G – серым.