Понятие амебы возникло в конце XX века для визуального упрощения комплексной поверхности. Определение амебы алгебраической гиперповерхности было впервые сформулировано в 1994 году в известной монографии Гельфанда-Капранова-Зелевинского[14], и вскоре обнаружилась удивительная фундаментальность этого понятия. Оно сыграло заметную роль в становлении такого раздела математики как тропическая геометрия, и получило важные применения в асимптотической теории и термодинамике, в теории димеров и компьютерной биологии.
Неудивительно, что ввиду фундаментальности понятие амебы могло возникнуть и в более ранних исследованиях, например, связанных с разложениями Лорана рациональных функций многих переменных, либо в попытках описать предельные положения алгебраических множеств (Бергман, [6], 1973 г). Со временем обнаружилось, что теория амеб представляет собой эффективный аппарат для изучения распределения нулей полиномов многих переменных, поскольку поведение «считающего» интеграла Иенсена-Ронкина для полинома в значительной мере определяется структурой амебы для гиперповерхности нулей полинома.
Вернемся к вопросу визуального упрощения комплексных поверхностей. Первый шаг в этом направлении был сделан Рейнхардтом, когда он предложил рассматривать двумерное комплексное пространство ℂ2 в системе «модулярных» координат |z1|, |z2|. В этих координатах пространство ℂ2 четырех вещественных переменных изображается квадрантом плоскости (диаграммой Рейнхардта), см. рис. 1.1.
Рассмотрим вопрос об изображении комплексной прямой 1 + z1 + z2 = 0 на диаграмме Рейнхардта. Запишем неравенства треугольника для каждой пары из трех комплексных чисел 1, z1, z2, участвующих в уравнении прямой:
![]()
Из них следует, что модули ri = |zi| координат точек (z1,z2), лежащих на прямой, удовлетворяют системе неравенств
![]()
Эта система определяет неограниченный прямоугольник (полуполосу), изображенный на рисунке 1.2.
Для каждой точки (r1,r2) указанного прямоугольника существует треугольник с длинами сторон 1, r1 и r2 (см. рис. 1.2). Расположим этот треугольник на комплексной плоскости пременного t так, чтобы в число его вершин входили t = 0 и t = 1. Если (r1,r2) — внутренняя точка прямоугольника, то интересующих нас треугольников два (см. рис. 1.3). Теперь понятно, как найти точки комплексной прямой, проектирующиеся в (r1,r2): это вектор (z1,z2) и сопряженный к нему вектор (1,2), изображенные на рисунке 1.4.

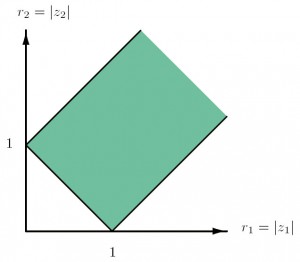
| 1.1 Диаграмма Рейнхардта | 1.2 Комплексная прямая на диаграмме Рейнхардта |
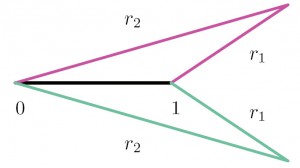
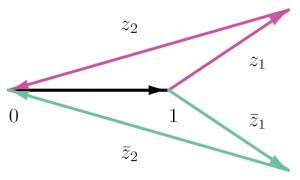
1.3. 1.4.
Таким образом, комплексная прямая изображается на схеме Рейнхардта неограниченным прямоугольником (см. рис. 1.2).
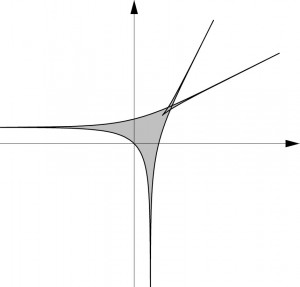
В результате логарифмической замены (r1,r2)-→(logr1, logr2) прямоугольник перейдет в фигуру, изображенную на рис. 1.5, которую называют амебой комплексной прямой.

1.5. Амеба комплексной прямой
Термин амеба выбран по той причине, что если комплексная кривая задается полиномиальным уравнением f(z1, z2) = 0 большой степени, то образ при отображении
представляет фигуру с тонкими щупальцами, уходящими в бесконечность, и, возможно, с конечным числом дырок. Таким образом, амеба комплексной кривой может принимать форму, схожую с биологической амебой (см. рис. 1.6).
1.6. Амеба комплексной кривой из ℂ2
Приведенные рассуждения для комплексной прямой естественным образом приводят к определению основного для нас объекта. Напомним, что комплексные алгебраические множества определяются системами полиномиальных уравнений.
Определение. Амебой алгебраического множества V ⊂ (ℂ \ 0)n называется его образ относительно логарифмического проектирования Log : (ℂ \ 0)n-→ℝn, определенного формулой
Амебу множества V будем обозначать АV . Если V — гиперповерхность, заданная нулями полинома f(z) = f(z1,…,zn), то мы также будем использовать для амебы обозначение Аf.
Заметим, что дополнение к амебе комплексной прямой состоит из связных компонент, каждая из которых открытая и выпуклая.
Оказывается, этот факт имеет место и для всякой гиперповерхности V = {f(z) = 0}, а именно, дополнение ℝn \A f амебы состоит из конечного числа связных компонент, каждая из которых открытая и выпуклая.
Открытость дополнения (или замкнутость самой амебы) следует из того, что отображение Log — собственное (прообраз каждой точки в ℝn есть вещественный n-мерный тор, т.е. компакт). Выпуклость связных компонент есть следствие фундаментального факта из многомерного комплексного анализа, гласящего, что область сходимости ряда Лорана для аналитической функции является логарифмически выпуклой. В рассматриваемой нами ситуации функция 1∕f(z) разлагается в ряд Лорана в области Log-1(E), где E — связная компонента дополнения к амебе, причем область сходимости этого ряда не может быть больше Log-1(E).
Отметим, что связные компоненты дополнения до изображения гиперповерхности на схеме Рейнхардта не обязательно выпуклые, что видно из примера комплексной гиперболы:
Её изображение на схеме Рейнхардта есть обычная гипербола r1r2 = 1, дополнение к которой состоит из двух связных компонент, причем одна из них не выпуклая. В то же время амеба гиперболы — прямая линия, поэтому ее дополнение до плоскости состоит из двух полуплоскостей, очевидно, выпуклых.
Понятие амёбы помогает исследовать дифференциально-геометрические свойства самих комплексных поверхностей. Основную роль в этом вопросе играет, так называемый, контур амебы — множество критических значений Log-отображения. Контур амебы вычисляется с помощью логарифмического отображения Гаусса для поверхности. Он содержит определенную информацию о дифференциально-геометрической структуре самой комплексной поверхности и структуре её сингулярной стратификации (с точки зрения микролокального анализа).
Дискриминант Δ(z1,z2) кубического уравнения y3 + z 2y2 + z 1y - 1 = 0 равен Δ(z1,z2) = 27 - 4z23 + 4z 13 + 18z 1z2 - z12z 22. Его амеба с выделенным контуром изображена на рис. 1.7. В отличие от амебы комплексной прямой (контур которой состоит из её топологической границы), контур амебы дискриминанта содержит внутреннюю часть — часть каспидальной кривой («клюва»), расположенную внутри амебы.
1.7. Амеба дискриминанта кубического уравнения
Природу клюва контура объясняет тот факт, что Log-проекция множества нулей дискриминанта имеет над острием клюва сингулярность типа «сборки»: вблизи прообраза острия эта проекция выглядит как на рис. 1.8, где поверхность в пространстве вещественных переменных p, q, x проектируется на плоскость переменных p, q так, что множество критических значений проекции есть полукубическая парабола.
1.8. Сингулярность проекции типа «сборки»
Свойство выпуклости каждой связной компоненты подмножества X из ℝn (или из любого векторного пространства) можно сформулировать на языке приведенных нульмерных групп гомологий. А именно, такое свойство равносильно тому, что для всякой прямой l ⊂ ℝnиндуцированный вложением гомоморфизм
является инъективным; последнее и означает, что если две точки из X можно соединить путем в X, то это же можно сделать на прямой l, проходящей через точки.
Пионерскими работами по теории амеб являются статьи Форсберга-Пассаре-Циха, [66], (2000) и Михалкина, [36], (2000).
После этих работ появилось множество других, связанных как с описанием самих амеб (Михалкин-Рульгорд [39], Энрикес [68], Теобальд [62]), так и с их применением в теории расширения неархимедовых полей (Айнзидлер-Капранов-Линд [19]), в теории димеров (Кеньон-Окуньков-Шеффилд [45]). Благодаря этим работам получило существенное развитие новое направление — тропическая геометрия (Капранов, Штурмфельс, Михалкин и другие).
В 2005 г. Лейнартасом-Пассаре-Цихом [29] теория амеб была применена к исследованию асимптотик многомерных разностных уравнений, играющих важную роль в теории обработки цифровых сигналов, в частности, при исследовании устойчивости цифровых рекурсивных фильтров.
Идеи работы [29] получили существенное развитие в построении термодинамики с несколькими гамильтонианами (многомерными спектрами, температурами, формами теплообмена).