Рассмотрим n таксонов. Расстояние между таксоном i и j есть действительное положительное число dij которое может быть определено некоторым биостатистическим методом. Получаем действительную симметрическую матрицу
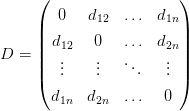
Определение 1. Матрица D представляет метрику если
![]()
![]()
![]()
Критерий того, что некоторая симметрическая матрица D является метрической матрицей можно сформуировать на языке тропической алгебраической геометрии.
Утверждение 1. Матрица D представляет метрику тогда и только тогда, когда D ⊙ D = D.
Доказательство. Покажем что если выполняется D ⊙ D = D, то матрица D является метрической. Тропическое умножение матриц происходит так же как и классическое, но с тропическими операциями сложения и умножения.
Пусть n = 3. Тогда D ⊙ D =
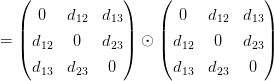
В результате умножения получаем матрицу:
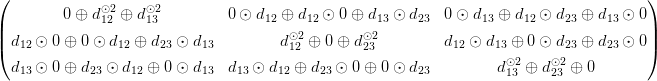
Выясним, при каких условиях D ⊙D = D. Рассмотрим элементы главной диагонали матрицы D ⊙ D
![]()
![]()
![]()
Это значит, что все не диагональные элементы матрицы D положительны.
Рассмотрим не диагональный элемент матрицы D ⊙ D:
![]()
![]()
![]()
Это значит, что для любого элемента dik, i≠k из матрицы D выполняется неравенство dik ≤ dij + djk, ∀j. По определению 14 получаем что матрица D – метрическая.
Аналогичные рассуждения проводятся для матриц любой размерности n.
Определение. Матрица D есть метрика дерева если существует дерево T с n листьями помеченными, положительными длинами всех граней и расстояние от листа i до листа j равно dij для всех i,j.
Оказывается, в большинстве случаев матрица D не является метрикой дерева. Поэтому возникает задача определить, при каких условиях матрица D задает метрику дерева.