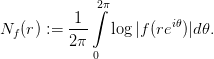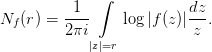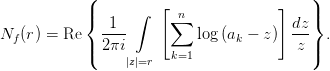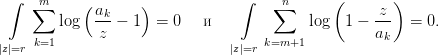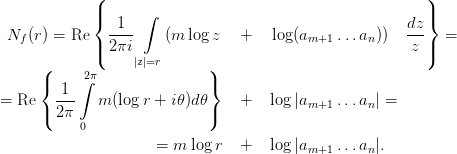Функция Иенсена-Ронкина

Приведем вначале классический результат Иенсена о распределении нулей полинома одного переменного (вместо полинома мы могли бы рассматривать голоморфную функцию в круге с центром в нуле, в частности, — целую функцию). Пусть f = (z - a₁)…(z - a_n) — полином, нули которого упорядочены по возрастанию модулей |a₁|≤… ≤|a_n|. Полиному f ставится в соответствие функция (интеграл) Иенсена

Заметим, что на окружности |z| = r

Поэтому функцию Иенсена мы можем представить в виде

Пусть f(0)≠0. Тогда имеет место следующая Формула Иенсена:

где m = m(r) – наибольший из индексов k, для которых |a_k| < r.

Для обоснования указанного равенства заметим, что по первоначальному определению функция Иенсена вещественная, поэтому

Таким образом, мы получаем интеграл от аналитической функции, хотя и многозначной:

По интегральной теореме Коши

В результате получаем

По формуле Виета произведение a₁…a_n = (-1)ⁿ равно f(0). Используя этот факт, а также свойства логарифмической функции, приходим к формуле Иенсена:

Заметим, что в промежутках между нулями полинома f функция N_f линейно зависит от log r (она равна m log r + const) и ее производная по log r равна m = m(r) — числу нулей полинома f(z) в круге |z| < r (см. рис. 2.1).

2.1. График функции N_f(log_r)

Поэтому N_f связана с логарифмическим вычетом соотношением

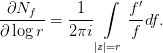
Наряду с указанными формами записи интеграла N_f удобна еще одна:

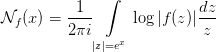
Многомерное обобщение функции Иенсена было введено Л.И. Ронкиным в 2001 г. Это обобщение мы называем функцией Иенсена–Ронкина. Она ставится в соответствие каждому полиному или ряду Лорана, сходящемуся в области Log^-1(Ω), где Ω ⊂ ℝⁿ – выпуклая область, и представляет собой интеграл

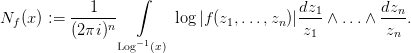
Следующие свойства функции N_f(x) были отмечены Л.И. Ронкиным (2001):

• (i) функция N_f(x) выпуклая;
• (ii) на каждой связной компоненте дополнения ℝⁿ \A_f амебы полинома f функция N_f(x) аффинно-линейная.

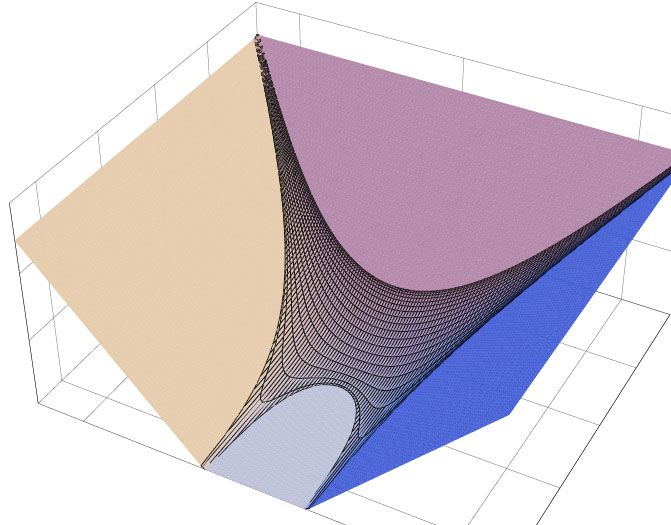
На рисунках 2.2 и 2.3 приведены примеры графиков функций Иенсена-Ронкина: затемненные части — это куски графиков над амебами многочленов, а остальные есть линейные куски над связными компонентами дополнений амёб.

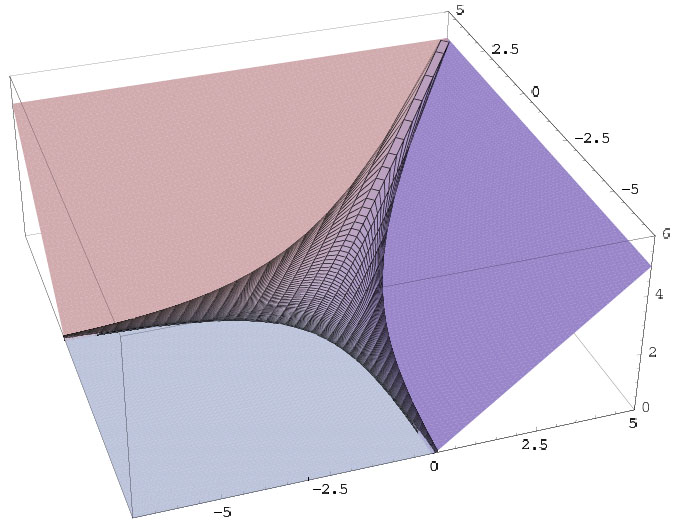
2.2. График функции Иенсена-Ронкина для полинома f(z) = 1 + z₁ + z₂.

2.3. График функции Иенсена-Ронкина для полинома

f(z) = z₁ - 5 - 2(z₂ + z₂^-1).