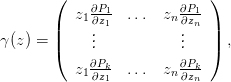Определение. [25, 8] Логарифмическим отображением Гаусса назовем отображение γ : V → Gr(n,k), которое каждой гладкой точке z ∈ reg V ставит в соответствие нормальное подпространство γ(z) к образу log V .
Лемма. Пусть V в окрестности гладкой точки задается нулями полиномов P1,…,Pk:
Тогда логарифмическое отображение Гаусса в этой точке задается матрицей
(3. 1)
вектор-строки которой образуют базис нормального пространства к образу log V .
Теорема. [8] Точка z ∈ reg V является критической для отображения Log тогда и только тогда, когда образ γ(z) логарифмического отображения Гаусса содержит
- хотя бы n - 2d + 1 линейно независимых над ℂ вещественных векторов при 2d ≤ n,
- хотя бы один вещественный вектор при 2d ≥ n.
В частности, в случаях гиперповерхностей (d = n- 1) и кривых (d = 1) точка z критическая тогда и только тогда, когда логарифмическое отображение Гаусса γ(z) вещественно.
Суть этого утверждения заключается в следующем. Отображение LogV : V → ℝn есть композиция комплексного логарифма
и проекции на вещественные координаты ℝn:
Комплексный логарифм локально биголоморфен в торе Tn и поэтому не имеет критических точек на reg V , следовательно, критические точки Log|V это критические точки проекции
Критические точки проекции определяются касательным отображением
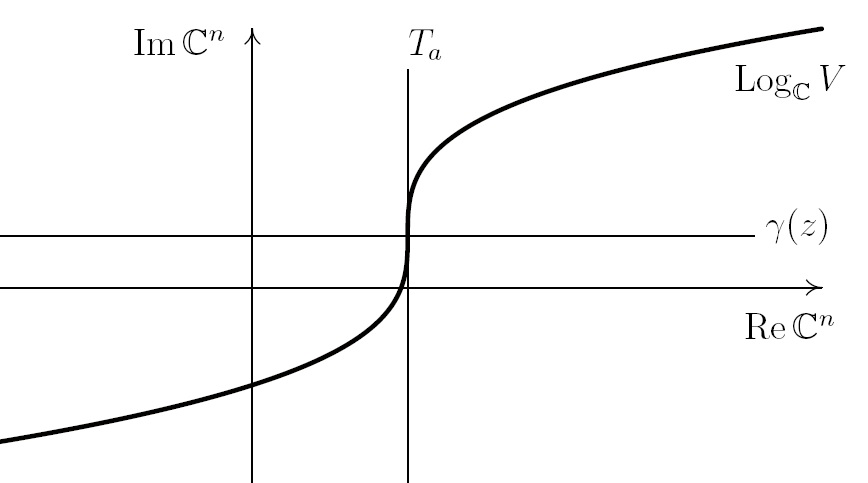
и связаны с тем, является ли нормальное пространство к LogℂV вещественным или нет. В каком-то смысле это иллюстрирует Рис. 3.2: в критических точках проекции πℝn нормальное подпространство γ(z) становится «горизонтальным» и не содержит вещественных точек, т.е. γ(z) вещественно.
3.2
3.3. Нормальные пространства к поверхности невырожденной и контуру вырожденной амеб комплексных прямых
Пример. В критической точке отображения Log комплексной прямой в ℂ3 (d = 1) оба вектора логарифмического отображения Гаусса γ(z) должны быть вещественными.
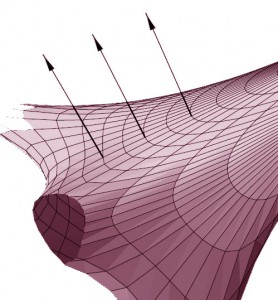
На рис. 3.3 слева изображена часть невырожденной, т.е. не имеющей контура, амебы комплексной прямой Касательное пространство в каждой точке такой амебы двумерно, следовательно, рассматриваемая в теореме проекция инъективна, поэтому критических точек нет, γ(z) содержит только один вещественный вектор, и в каждой точке амебы мы можем построить лишь одномерные нормали к ней.
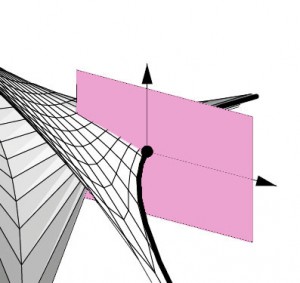
Пример. Справа на рис. 3.3 изображена амеба вырожденной комплексной прямой.
В точках края амебы инъективность проекции π ℝ3Tw(log V ) нарушена, следовательно, эти точки являются точками контура. В таких точках γ(z) содержит уже два вещественных вектора. Cоответственно, двумерно нормальное пространство к амебе, которое является вещественной проекцией задаваемого с помощью γ(z) комплексного нормального к log V пространства.