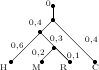
Филогенетическое дерево является одной из важнейших математических структур в биологии.
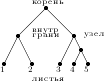
Введем необходимые математические понятия для описания задачи построения филогенетического дерева. Термин n-дерево будет означать дерево (т.е. связный граф без циклов) с отделенной вершиной степени 2, называемой корнем и n вершин степени 1, называемыелистьями. Мы будем рассматривать бинарные деревья (т.е. деревья чьи корни имеют степень 2 и все вершины степени 1 или 3). Узлом дерева будем называть вершину степени 3. Внутренняя грань дерева - это грань, которая не соединена с листом. Метрическое n-дерево это дерево с положительными длинами всех граней. Далее слово дерево означает метрическое n-дерево.
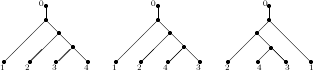
Для удобства будем строить деревья с еще одной нулевой вершиной, растущей из корня. Заметим, что одно и тоже дерево можно построить разными способами. Ниже на рисунке изображено одно и тоже дерево тремя способами.
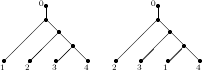
С другой стороны, деревья одинаковой структуры но с разными листьями различны. Количество различных бинарных деревьев с количеством листьев n равно (2n - 3)!!.
Так как дерево это граф без циклов, значит существует только один путь от листа i до листа j. Растоянием между двумя листьями будем считать сумму длин всех граней лежащих между этими листьями.
Каждому n-дереву соответствует симметрическая матрица с нулями на главной диагонали размерности n:
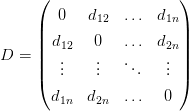
Элемент матрицы dij есть расстояние от листа i до листа j.
Пример построения филогенетического дерева по
ДНК-последовательностям
Для определения родства между человеком, мышью, кроликом и цыпленком биологи рассмотрели последовательности геномов следующего вида:
H: ACAATGTCATTAGCGAT…
M: ACGTTGTCAATAGAGAT…
R: ACGTAGTCATTACACAT…
C: GCACAGTCAGTAGAGCT…
Из этих наборов биологи вычислили расстояния между любыми двумя таксонами. Существуют различные алгоритмы для этого вычисления, основанные на статистических моделях эволюции.
Для нашего примера матрица расстояний имеет следующий вид:

По этой матрице можно восстановить дерево: