Амебы сингулярных стратов классического дискриминанта

С общим алгебраическим уравнением

(3 .7)

тесно связан многочлен Δ от переменных a = (a₀,…,a_n) — дискриминант уравнения.

Он «отвечает» за наличие кратных корней в том смысле, что Δ(a) = 0 в том и только том случае, когда уравнение  имеет по крайней мере один кратный корень. Дискриминант Δ является неприводимым многочленом с целыми коэффициентами, определен однозначно, с точностью до выбора знака, и может быть выражен через корни r₁,r₂,…,r_n уравнения при помощи формулы

Следуя [14, глава 12], мы будем считать знак в дискриминанте равным (-1)^n(n-1)∕2.

Классический определитель Сильвестра дает явное выражение для дискриминанта через коэффициенты уравнения:

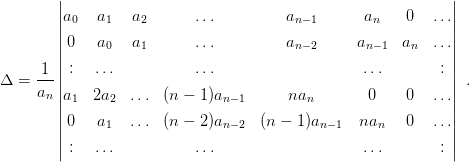
(3 .8)

Для n = 2 эта формула дает Δ = 4a₀a₂ - a₁², для n = 3

Число слагаемых в Δ быстро растет с увеличением n, равно как и абсолютные величины коэффициентов в этих слагаемых. При n = 4 дискриминант содержит 16 мономов, в то время как при n = 5 их число равно 59.

Для любого n мономы nⁿa ₀^n-1a _n^n-1 и Бa ₁²a ₂²…a _n-1² присутствуют в Δ.

Дискриминант уравнения мы называем классическим. Обозначим через ∇ его нулевое множество и будем его называть дискриминантным множеством уравнения или многочлена f.

Геометрически гиперповерхность ∇ есть двойственное многообразие для кривой Веронезе [1 : t : t² : … : tⁿ] в ℂℙⁿ. Иными словами, она состоит из тех векторов a ∈ ℂ¹⁺ⁿ, для которых соответствующая гиперплоскость a₀z₀ + a₁z₁ + … + a_nz_n = 0 не трансверсальна параметризованной кривой z_ν = t^ν (см. [14]).

Рассмотрим подмножества M^j ⊂∇, состоящие из таких a ∈ ℂⁿ⁺¹, для которых уравнение имеет корни кратности ≥ j. Эти подмножества образуют вложенную цепочку

Каждое M^j+1 принадлежит множеству сингулярных точек sng M^j, при этом страт S^j = M^j \M^j+1 состоит из точек, где M^j либо неособо, либо самопересекается своими гладкими кусками. Поэтому мы называем M^j сингулярными стратами каспидального типа. Такие страты впервые рассматривались в работе Д. Гильберта [17], см. также [27]. Здесь мы изложим недавние наблюдения Е.Н. Михалкина и А.К. Циха [41].

Определенную информацию о приведенном дискриминантном множестве и его сингулярных стратах можно получить в логарифмической шкале в терминах понятия амебы алгебраической поверхности. В случае, когда алгебраическое множество V есть гиперповерхность или кривая, ее неособая точка z является критической для Log|_V в том и только том случае, когда логарифмическое отображение Гаусса в ней вещественно (см. [36]). Таким образом, для V = ∇_pq контур амебы параметризуется сужением отображения Ψ_{pqMℝℙ^n-2} на вещественное проективное подпространство. Аналогично, контур амебы для страта M_pq^n-1 параметризуется сужением Ψ _pq на вещественный срез L^n-3 ∩ ℝℙ^n-2.

Рассмотрим в качестве примера приведенное дискриминантное множество ∇₀₄ для уравнения степени 4. Согласно теоремам ?? и ?? его страт M₀₄³ параметризуется сужением параметризации

на комплексную прямую своих критических точек

Выбрав s₁ в качестве аффинной координаты на L₁, сужение Ψ_04L¹ можно представить в виде

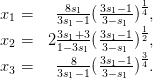
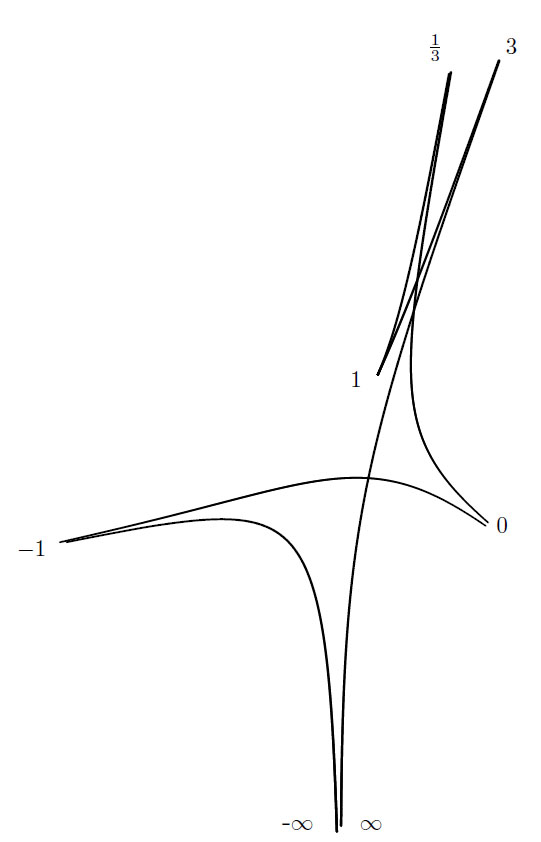
3.6. Контур амебы страта M₀₄³ для уравнения степени 4

Разные положения контура амебы страта M₀₄³ для уравнения степени 4

На 3.6 изображен контур для страта M₀₄³, допускающего указанную параметризацию.

Из параметризации видно, что щупальца амебы соответствуют набору значений s₁ = -∞,  - 1, 0, 1/3, 3.

Значению s₁ = 1 соответствует нульмерный страт M₀₄⁴; это критическая точка параметризации. Таким образом, контур амебы нульмерного страта M₀₄⁴ является точкой возврата (каспидальной точкой) для контура амебы примыкающего к нему одномерного страта M₀₄³.

Чтобы проследить характер примыкания контуров амеб стратов M₀₄² = ∇ ₀₄ и M₀₄³, требуется определенная деликатность. В аффинных координатах s₁,s₂ пространства ℂℙ² параметризация Ψ ₀₄ для M₀₄² = ∇ ₀₄ следующая:

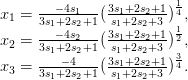
Для построения контура амебы надо вычислить образ ℝ² ⊂ ℝℙ² относительно отображения Log ∘ Ψ₀₄. Это отображение имеет полярные особенности на четырех прямых (пятая прямая s₃ = 0 является бесконечно удаленной относительно выбранной аффинной части):

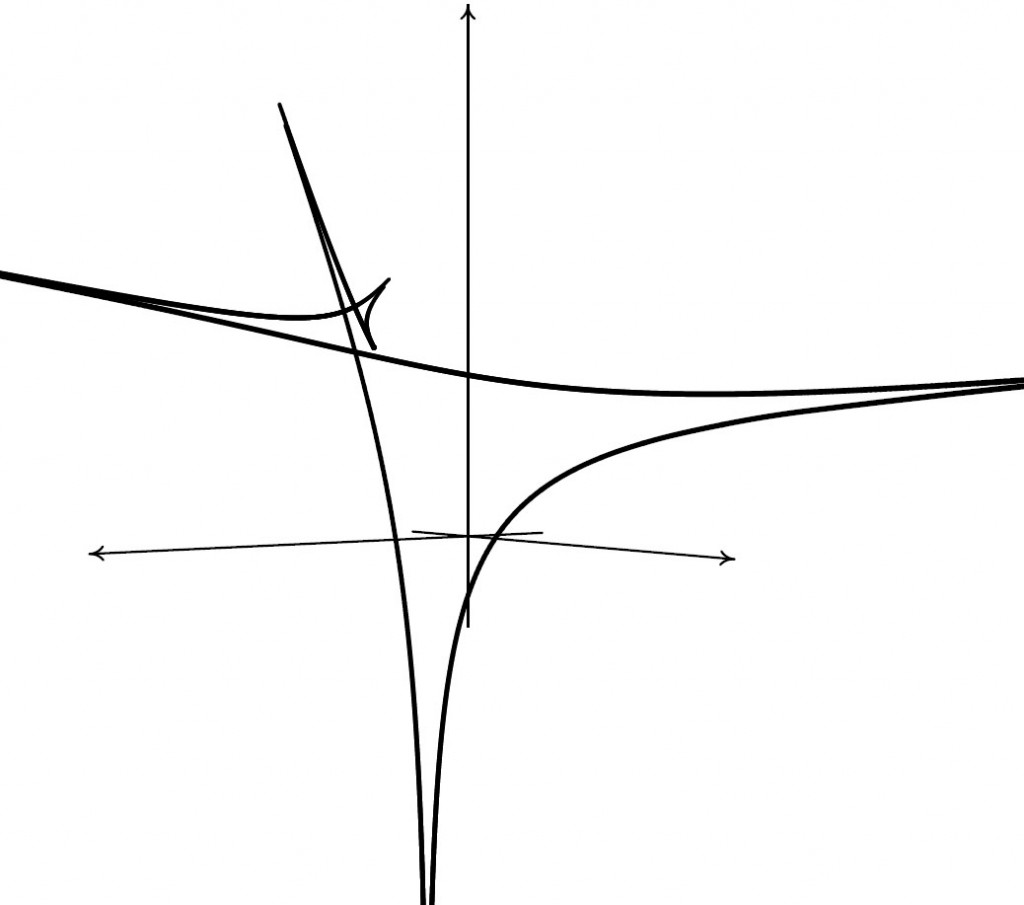
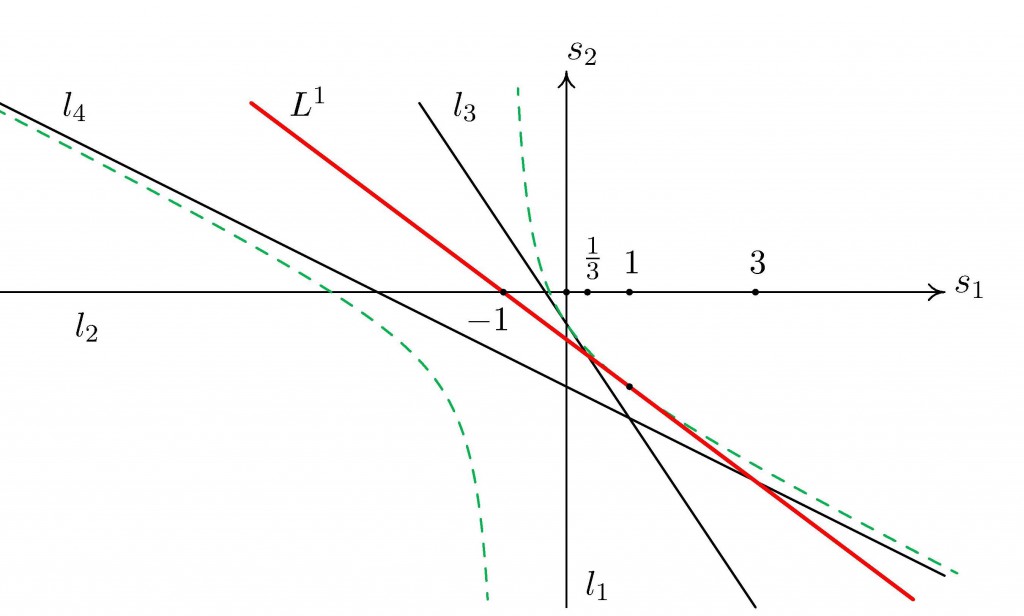
Рис. 3.7. Особенности параметризации Ψ₀₄: 4 полярных прямых, критическая прямая и гипербола самопересечений

На рис. 3.7 эти прямые изображены наряду с критической прямой L¹ (жирная прямая, переходящая при отображении Log ∘ Ψ₀₄ в контур амебы для M₀₄³). Кроме того, следует учесть роль гиперболы {(s₁ + 1)(s₁ + 2s₂ + 3) = 2}, изображенной пунктиром. Образ комплексной гиперболы относительно Ψ₀₄ есть страт M₀₄^2,2, отвечающий за наличие двух корней кратности 2. Иными словами, этот страт состоит из всех x = (x₁,x₂,x₃), для которых выполняется равенство многочленов

с параметрами a и b. Обозначив t := a + b, зададим этот страт при помощи параметризации x₁ = ∓2t, x₂ = t² Б 2, x ₃ = -2t. Множество M₀₄^2,2 составляет страт самопересечения для дискриминантного множества ∇₀₄. Сужение параметризации Ψ₀₄ на указанную гиперболу принимает равные значения в точках (s₁,s₂), (s′₁,s′₂), для которых s₁ ⋅ s′₁ = 1.

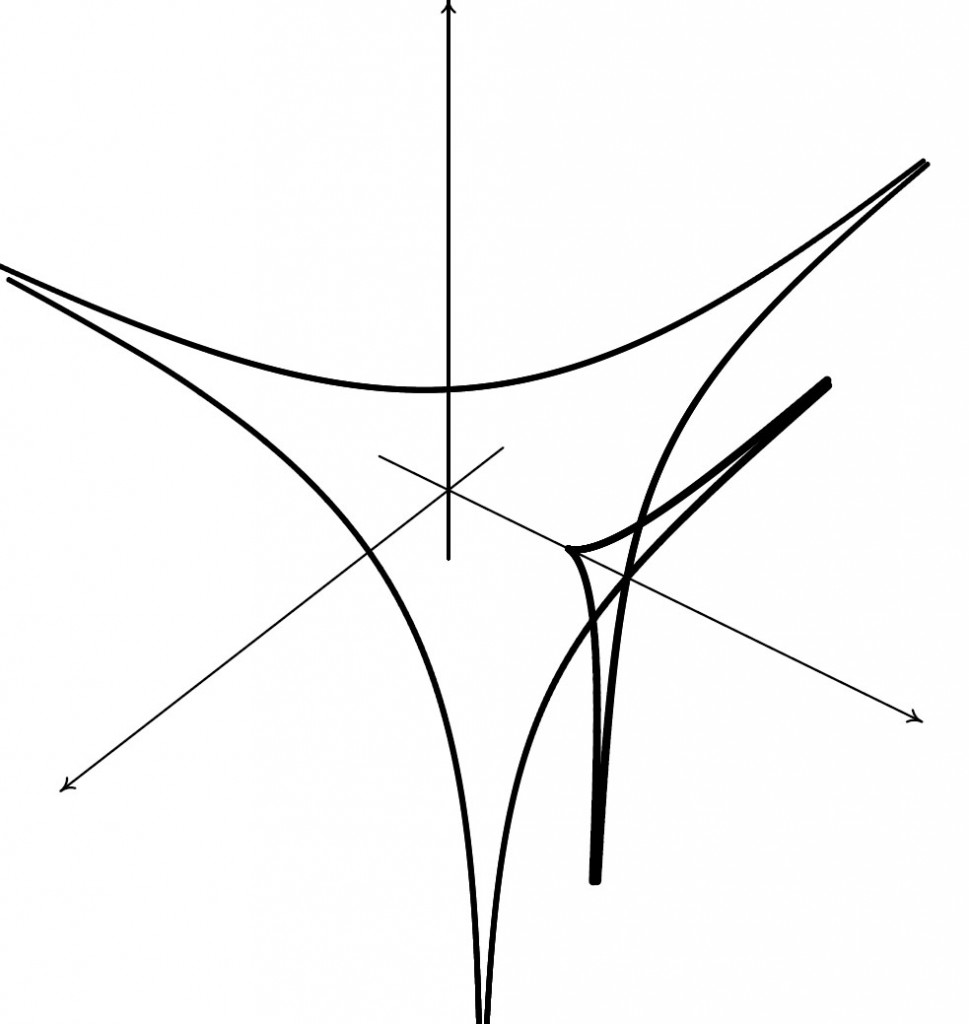
На рис. 3.8 приводятся некоторые фрагменты примыканий контура амебы для ∇₀₄ к контуру амебы для страта M₀₄³ в разных ракурсах.

Они показывают, что контур амебы для страта M₀₄³ является кривой возврата контура амебы для ∇₀₄. Вблизи острия контура для амебы M₀₄³ (соответствующему значению s₁ = 1 в параметризации контура) примыкание изображается куском в виде сетки и скрытыми за ней двумя возвратными кусками серого цвета. Эти куски пересекаются в общем положении по кривой, которая выходит из острия и представляет часть контура амебы для страта самопересечения M₀₄^2,2.

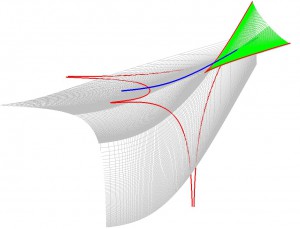
3.8. Фрагменты примыкания контура амебы для ∇₀₄ к контуру амебы для страта M₀₄³

В целом, поверхность справа составляет фигуру, известную под названием «ласточкин хвост». Она получается как часть контура амебы для ∇₀₄, для которой вещественные аффинные параметры s₁,s₂ пробегают подходящим образом выбранную окрестность луча L¹ ∩{s ₁> 0}.