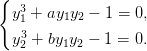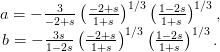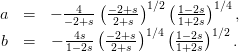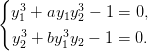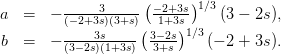Рассмотрим полиномиальное отображение
где Tn = ![]() n — комплексный алгебраический тор, а P i — полиномы Лорана, т.е. полиномы от переменных y1, y1-1,…, y n, yn-1. Будем считать, что множества A(i) показателей мономов в P i фиксированы, а все коэффициенты переменные. В таком случае будем говорить, чтоP – общее полиномиальное отображение из Tn в ℂn.
n — комплексный алгебраический тор, а P i — полиномы Лорана, т.е. полиномы от переменных y1, y1-1,…, y n, yn-1. Будем считать, что множества A(i) показателей мономов в P i фиксированы, а все коэффициенты переменные. В таком случае будем говорить, чтоP – общее полиномиальное отображение из Tn в ℂn.
Для таких отображений обозначим через ∇0 множество всех коэффициентов, при которых P имеет в Tn кратные нули, т.е. нули, в которых якобиан P равен нулю.
Определение. Дискриминантным множеством ∇ отображения P назовем замыкание множества ∇0 в пространстве коэффициентов.
Таким образом, для нас представляет интерес система полиномиальных уравнений вида
(3. 9)
с неизвестными y = (y1,…,yn) ∈ Tn и переменными коэффициентами a λ(i), где A(i) ⊂ ℤn – фиксированные конечные подмножества, λ = (λ 1,…,λn), yλ = y 1λ1…y nλn.
Как и в случае n = 1 общую систему алгебраических уравнений можно свести к приведенному виду, где в каждом уравнении фиксированы по два коэффициента (см. [2]).
Здесь мы проиллюстрируем некоторые преимущества параметрического задания дискриминантных множеств перед заданием в вида уравнения. Речь идет о расположении дискриминантного множества, которое мы рассматриваем в логарифмической шкале, т.е. в виде амёбы этого множества.
Рассмотрим примеры приведенных систем.
Пример.
Рассмотрим систему уравнений вида
Для нее параметризация дискриминантного множества имеет вид:
(3. 10)
Исключив параметр s из параметризации (3.10), получим приводимый полином двух переменных a, b:
где D(a,b) – это полином
a ε1 = e![]() , ε2 = e
, ε2 = e![]() . Этот полином D(a,b) и есть дискриминант.
. Этот полином D(a,b) и есть дискриминант.
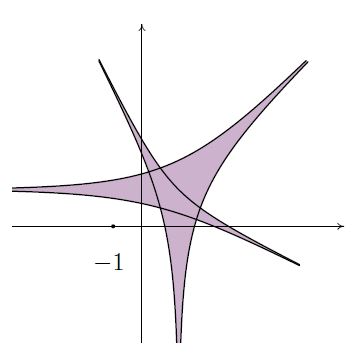
На рисунке 3.9 изображена амеба дискриминантного множества ∇, где выделенные линии составляют контур амебы. Из рисунка видно, что нормаль к контуру амебы при полном его обходе делает один оборот (т.е. пробегает ℝℙ1), и это подчеркивает, что параметризация Δ является обратным отображением к логарифмическому отображению Гаусса для ∇.
3.9. Амеба дискриминанта и ее контур
Пример. Рассмотрим систему уравнений вида
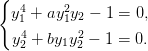
Для нее параметризация дискриминантного множества имеет вид:
(3. 11)
Исключив параметр s из параметризации (3.11), получим полином двух переменных a, b (дискриминант):
Пример. Рассмотрим систему уравнений вида
Для нее параметризация дискриминантного множества имеет вид:
(3. 12)
Амеба дискриминанта данной системы изображена на рисунке 3.10.
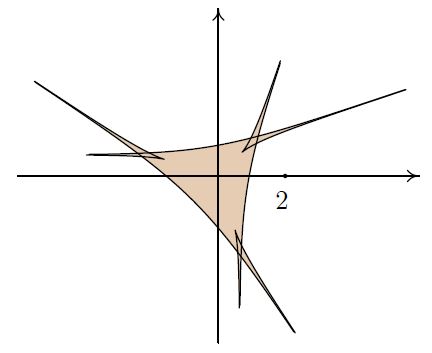
3.10. Амеба дискриминанта и ее контур
Исключив параметр s, получим полином двух переменных a, b:
Теперь становится очевидным, что по такому уравнению мы вряд-ли смогли бы построить амёбу его множества решений.