Тропические полиномы и их графики | Амёбы комплексных аналитических множеств

Пусть x₁,x₂,…,x_n — переменные, принимающие значения в тропическом полукольце.

Тропический моном определяется как тропическое произведение коэффициента и тропических степеней переменных x_i:

где a_{i₁…i_n} ∈ ℝ; i_k ∈ ℤ,k = 1,…,n. Он представляет собой функцию из ℝⁿ ⇒ ℝ :

Например:

Таким образом, с точки зрения классической математики тропические мономы — это в точности линейные функции с целыми коэффициентами при x_i.

Определение. Тропический полином — это конечная линейная тропическая комбинация тропических мономов

(4. 1)

где a_i^k = a_{i₁^k…i_n^k} ∈ ℝ; x^{⊙i^k} = x₁^{⊙i₁^k}…x_n^{⊙i_n^k}.

Тропический полином — это функция ℝⁿ → ℝ, которая с точки зрения классической арифметики есть максимум конечного числа линейных функций:

где x = (x₁,…,x₂) ∈ ℝⁿ; i^k = (i₁^k,…,i_n^k) ∈ ℤⁿ.

Для двух переменных:

где a_i^k ∈ ℝ, i_n^k ∈ ℤ, k = 1,…,n.

Тропическая функция обладает тремя важными свойствами:

p непрерывна.
p кусочно-линейная, где количество кусков конечно.
p вогнута, т.е p(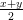) ≤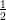(p(x) + p(y)).

Каждая функция, которая удовлетворяет свойствам 1)-3), может быть представлена в виде максимума конечного числа линейных функций.

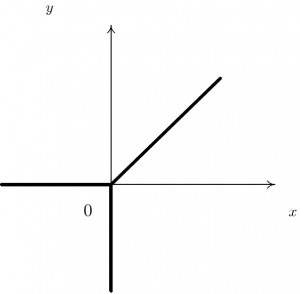
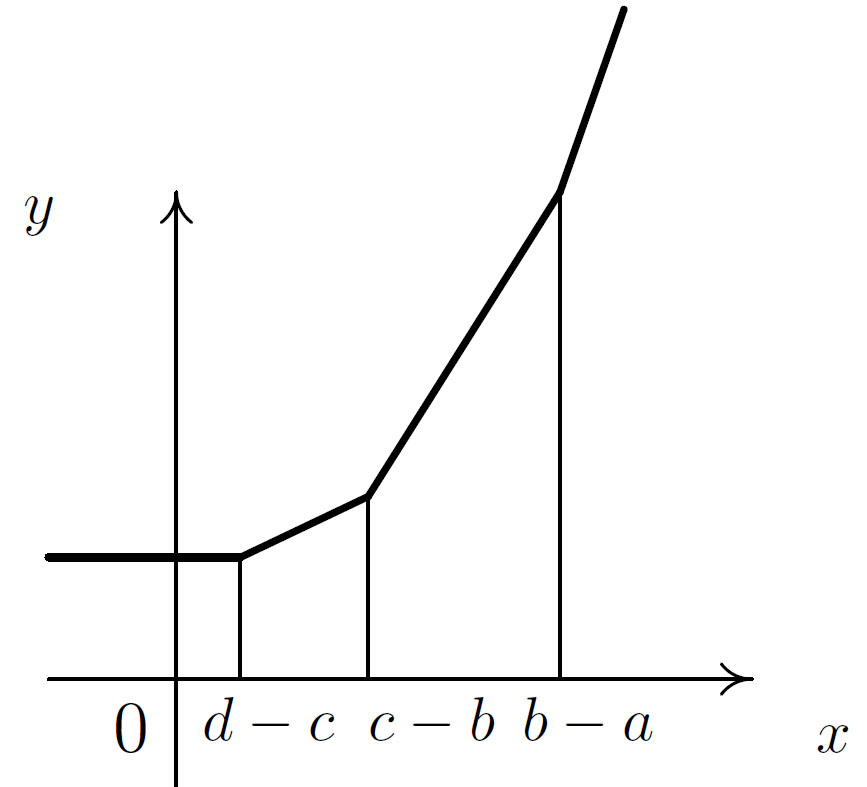
В качестве примера рассмотрим график тропического кубического многочлена одной переменной

изображеный на рисунке 4.1. Значения функции p_t(x) находятся как максимум четырех линейных функций

Более точно, значение функции p_t(x) — это наибольшее из значений y таких, что пара (x,y) лежит на одной из четырех прямых. Таким образом, график p_t(x) есть верхняя огибающая этих четырех прямых. Все четыре линии вносят вклад, если b - a > c - b > d - c. Точки x = b -a, x = c - b, x = d - c являются точками излома графика, в которых p_t(x) не линейна.

4.1. Кривая и график тропической функции (4.3)

Точки излома берутся в качестве корней тропического полинома. На первый взгляд это выглядит странно. Однако, если мы вспомним график функции Иенсена (см. п. 2.1.), которая в переменной log|z| также кусочно-линейна и терпит излом в момент появления корней многочлена, то такая идея становится естественной. При этом мы можем определить нулевое множество тропического многочлена любого числа переменных, т.е. тропическую гиперповерхность.

Определение. [61] V (p_t) называется множество всех точек x ∈ ℝⁿ, в которых максимум достигается одновременно не менее, чем на двух линейных функциях, задающих тропическую функцию p_t(x).

Иными словами, точка x ∈ ℝⁿ принадлежит V (p_t) тогда и только тогда, когда p не линейна в этой точке.

Рассмотрим случай n=2. Тропический полином в этом случае будет иметь вид:

(4.2)

Соответствующая многочлену 4.2 тропическая гиперповерхность называется плоской тропической кривой. Следующее предложение определяет характерные особенности такой тропической кривой.

Предложение. Кривая V (p_t) — это конечный граф, который вложен в плоскость ℝ². Он имеет ограниченные и неограниченные грани, углы наклона всех граней рациональные.

Пусть p_t — произвольный тропический многочлен от x и y. Рассмотрим все слагаемые a_ij ⊙x^⊙i ⊙y^⊙j, содержащиеся в p_t. В классической арифметике каждое слагаемое представляет линейную функцию a_ij + ix + jy от x и y. Тропическая функция p_t : ℝ² → ℝ данной точке ставит в соответствие максимум этих линейных функций.

Пример. График тропического полинома

(4.3)

изображен на рисунке ??. Согласно определению 4.1.2,

Для того, чтобы построить этот график по определению, для двух любых наборов (i^*,j^*) и (i′,j′) необходимо решить систему линейных уравнений и неравенств

где (i,j) ∈ Δ_{p_t}.

Решением этой системы является точка, отрезок, луч или пустое множество. Объединение этих точек, лучей и отрезков есть тропическая кривая, изображенная на рисунке 4.2. По графику наглядно видно, что тропическая кривая — это проекция на плоскость (x,y) точек, в которых функция p(x,y) не гладкая (график p(x,y) терпит излом).

4.2. Кривая и график тропической функции (4.3)