С каждой амебой Af ассоциируются две вещественные гиперповерхности, лежащие в Af, называющиеся спайн амебы и контур амебы.
Пусть A′⊂ ℝn ∩ Δ f состоит из таких векторов α, для которых амеба Af определяемая полиномом (??), имеет компоненты дополнения Eα порядка α.
Заметим, что согласно Лемме 1, множество A′ обязательно содержит все вершины многогранника Ньютона Δf.
Для каждого α ∈ A′ определим вещественное число aα следующим образом :
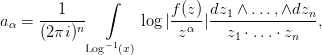
(4.5)
где x ∈ Eα.
Если α — вершина многогранника Ньютона Δf, то
![]()
(4.6)
но в общем случае aα сложным образом зависят от коэффициентов {cα} полинома f.
Рассмотрим кусочно-линейную функцию Sf : ℝn → ℝ, действующую по правилу
![]()
(4.7)
где aα находятся по формулам 4.5 и 4.6.
Определение. Множество точек x ∈ ℝn, в которых S f(x) негладкая, называется спайном амебы Af.
Поскольку Sf(x) — кусочно-линейная функция, определение 2.5, эквивалентно тому, максимум в (4.7) достигается одновременно хотя бы для двух функций {< α,x > +aα}.
Теорема. Спайн амебы Af есть ее строгий деформационный ретракт.
Поскольку многочлен, определяющий спайн амебы Af , задается как максимум линейных функций с целыми коэффициентами, он представляет собой тропический полином:
![]()
Поэтому спайн амебы можно интерпретировать как тропическую гиперповерхность и использовать для его исследования и построения все средства тропической алгебраической геометрии.
Так в случае n = 2 спайн амебы есть тропическая кривая в ℝ2, состоящая из лучей и отрезков прямых (см. рис. 4.7–4.9).
Предсказать форму этой кривой возможно, владея информацией о подразбиении многоугольника Ньютона. Однако для этого необходимо знать коэффициенты aα тропического полинома Sf(x), в общем случае связанного с коэффициентами исходного полинома Лoрана fсоотношениями (4.5). Вычисление этих коэффициентов представляет собой достаточно сложную задачу.