Пусть X = (Xij) – некоторая симметрическая матрица с нулями на диагонали и неизвестными Xij, i≠j. Каждой четверке {i,j,k,l}⊂{1, 2,…,n} поставим в соответствие следующий полином степени 2 по правилу
Это отношение определяет гиперповерхность T(pijkl) в пространстве ℝ
. Тропический Грассманиан есть пересечение этих гиперповерхностей. Это есть полиэдральный веер определенный как:
Рассмотрим случай n = 4.
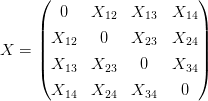
Получаем одно соотношение
Значит, тропический грассманиан Gt2,4 состоит из одной тропической гиперповерхности T(p1234).
В этом случае тропический грассманиан Gt2,4 есть тропическая гиперповерхность полинома 
1234 = X12X34 + X13X24 + X14X23, где 1234 – есть плюкерово соотношение классического грассманиана G1,3.
Согласно [61] в случае неархмедова нормирования амёба A(V ) гиперповерхности
совпадает с T(trop(1234)), и значит тропический грассманиан Gt2,4 есть амёба гиперповерхности V .
Основная теорема о пространстве филогенетических деревьев состоит в следующем.
Теорема. Метрическая матрица D задает метрику дерева тогда и только тогда, когда матрица X = -D есть точка в тропическом Грассманиане Gr2,n.
Пример. Рассмотрим случай n = 4 разобраный в п.2.3. Матрица D=
Тропический грассманиан есть тропическая гиперповерхность T(p1234), где
Матрица X = -D =
Подставим элементы матрицы X в p1234:
Матрица X есть точка в тропическом грассманиане, значит X задает метрику дерева.